What Optimization Should We Work On (Lean Software Development Part 5)

At work, we are building a risk aggregation system. As it’s dealing with a large bunch of numbers, it’s a huge heap of optimizations. Once that its most standard features set is supported, our job mostly consists of making it faster.

That’s were we are now doing.

How do we choose which optimization to work on ?

The system still being young, we have a wide range of options to optimize it. To name just a few : caches, better algorithms, better low level hardware usage …

It turns out that we can use the speedup factor as a substitute for business value and use known techniques to help us to make the best decisions.

Let’s walk through an example

I. List the optimizations you are thinking of

Let’s suppose we are thinking of the following 3 optimizations for our engine

• Create better data structures to speed up the reconciliation algorithm
• Optimize the reconciliation algorithm itself to reduce CPU cache misses
• Minimize boxing and unboxing

II. Poker estimate the story points and speedup

Armed with these stories, we can poker estimate them, by story points and by expected speedup. As a substitute for WSJF, we will then be able to compute the speedup rate per story point. We will then just have to work on the stories with the highest speedup rate first.

Title	Story Points	/10	/2	-10%	~	+10%	x2	x10	Expected Speedup ratio*	Speedup rate / story point**
Data Structures	13					4 votes	5 votes		x 1.533	x 1.033
Algorithm	13		1 vote	1 vote	2 votes	1 vote	2 votes	2 votes	x 1.799	x 1.046
Boxing	8					9 votes			x 1.1	x 1.012

^{* Expected speedup ratio is the logarithmic average of the voted speedups
** Speedup rate is “speedup(1/ story points)“}

So based on speedup rate, here is the order in which we should perform the stories :

1. Algorithm
2. Data Structures
3. Boxing

III. And what about the risks ?

This poker estimation tells us something else …

We don’t have a clue about the speedup we will get by trying to optimize the algorithm !

The votes range from /2 to x10 ! This is the perfect situation for an XP spike.

Title	Story points	Expected Speedup rate
Algorithm spike : measure out of context CPU cache optimization speedup	2	?

In order to compute the expected speedup rate, let’s suppose that they are 2 futures, one where we get a high speedup and another where we get a low one.

They are computed by splitting the votes in 2 :

• low_speedup = 0.846
• high_speedup = 3.827

If the spike succeeds

We’ll first work on the spike, and then on the algorithm story. In the end, we would get the speedup of the algorithm optimization.

• spike_high_speedup = high_speedup = 3.827

If the spike fails

We’ll also start by working on the spike. Afterwards, instead of the algorithm story, we’ll tackle another optimization stories, yielding our average speedup rate for the duration of the algorithm story. The average speedup rate can be obtained from historical benchmark data, or by averaging the speedup rate of the other stories.

• average_speedup_rate = (1.033 * 1.011)^1/2 = 1.022
• spike_low_speedup = average_speedup_rate^story_points = 1.02213 = 1.326

Spike speedup rate

We can now compute the average expected speedup rate for the full period ‘spike & algorithm’ stories. From this we will be able to get the speedup rate and finally, to prioritize this spike against the other stories in our backlog.

• spike_speedup = (spike_low_speedup * spike_high_speedup)^1/2 = 2.253
• spike_speedup_rate = spike_speedup^{1/(spike_story_points + algorithm_story_points)} = 2.253^{1/(2 + 13)} = 1.056

IV. Putting it all together

Here are all the speedup rate for the different stories.

Title	Speedup rate / story point
Data Structure	x 1.033
Algorithm	x 1.046
Boxing	x 1.012
Algorithm spike	x 1.056

Finally, here is the optimal order through which we should perform the stories :

• Algorithm spike
• Algorithm (only if the spike proved it would work)
• Data Structures
• Boxing

Summary

The math are not that complex, and a simple formula can be written to compute the spike speedup rate :

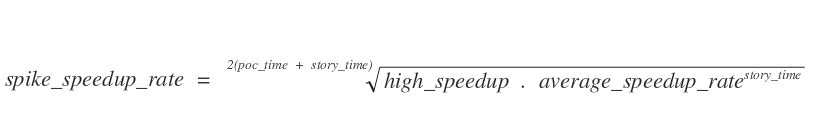
I think most experienced engineers would have come to the same conclusion by gut feeling …

Nevertheless I believe that systematically applying the such method when prioritizing optimizations can lead to a greater speedup rate than the competition in the long run. This is a perfect example where taking measured risks can payoff !

This was part 5 of my Lean Software Development Series. Part 4 was Measure the business value of your spikes and take high payoff risks, Part 5 will be You don’t have to ask your boss for a fast build.

Stay up to date with content and upcoming products

I usually write about 15 minutes worth of reading per month. I won't transfer your email. No Spam, unsubscribe whenever you want.

As a gift for subscribing, you'll receive an illustrated mini-ebook "How to start a team coding dojo"!